POLINÔMIOS PROGRESSIMAIS GRACELI.

 PARA TODO E QUALQUER POLINÔMIO COM [N] SE TROCARA POR UMA FUNÇÃO PROGRESSIMAL GRACELI = P.

OU SEJA, 

N = P

POLINÔMIOS PROGRESSIMAIS GRACELI.

julho 13, 2021

 POLINÔMIOS PROGRESSIMAIS  GRACELI.

ONDE OS POLINÔMIOS SÃO ACRESCIDOS DE FUNÇÕES PROGRESSIMAIS.

COMO:

P = PW / PY] =

                                                   

                                                    P

P = PW / PY] [PS /K] + [PR/ PQ]   =

VEJAMOS COMO FICA EM ALGUNS POLINÔMIOS.

Função polinomial

Origem: Wikipédia, a enciclopédia livre.

 Nota: "Polinômio e Polinómio" redirecionam para este artigo. Para outros significados, veja Polinomial.

Gráfico de uma função polinomial

Em matemática, função polinomial é uma função ${\displaystyle P}$ que pode ser expressa da forma:^[1][2][3][4]

${\displaystyle P\left(x\right)=a_{n}x^{n}+a_{n-1}x^{n-1}+\dots +a_{1}x^{1}+a_{0}x^{0}=}$ ${\displaystyle \sum _{i=0}^{n}a_{i}x^{i},}$ [[+, - , * , / ] P

em que ${\displaystyle n}$ é um número inteiro não negativo e os números ${\displaystyle a_{0},a_{1},...a_{n-1},a_{n}}$ são constantes, chamadas de coeficientes do polinômio.

• 
  

Grau de uma função polinomial

Ver artigo principal: Função homogênea

As funções polinomiais podem ser classificadas quanto a seu grau. O grau de uma função polinomial corresponde ao valor do maior expoente da variável do polinômio, ou seja, é o valor de ${\displaystyle n}$ da função ${\displaystyle P\left(x\right)=\sum _{i=0}^{n}a_{i}x^{i}.}$ [[+, - , * , / ] P

Sejam ${\displaystyle f(x)}$ e ${\displaystyle g(x)}$ polinômios de graus quaisquer. Sempre valem as seguintes leis:^{[Nota 1]}

• O grau de ${\displaystyle f(x).g(x)}$ é a soma do grau de ${\displaystyle f(x)}$ e o grau de ${\displaystyle g(x);}$
• Se ${\displaystyle f(x)}$ e ${\displaystyle g(x)}$ têm grau diferente, então o grau de ${\displaystyle f(x)+g(x)}$ é igual ao maior dos dois; e
• Se ${\displaystyle f(x)}$ e ${\displaystyle g(x)}$ têm o mesmo grau, então o grau de ${\displaystyle f(x)+g(x)}$ é menor ou igual ao grau de ${\displaystyle f(x).}$

Funções polinomiais de grau um

Ver artigo principal: Função polinomial de primeiro grau

Gráfico de uma função do 1º grau^[5]

Aqui, ${\displaystyle n=1.}$ Por isso, os polinômios de grau 1 têm a forma ${\displaystyle P\left(x\right)=a_{0}x^{0}+a_{1}x^{1}=a_{0}+a_{1}x.}$

As funções deste tipo são chamadas de função afim. Se ${\displaystyle a_{0}=0,}$ chamamos esta função afim de linear.^[2][4]

Por exemplo, ${\displaystyle f(x)=2x+1}$ é uma função polinomial de grau um composta de dois monômios.

Funções polinomiais de grau dois

Ver artigo principal: Função quadrática

Gráfico de uma função do 2º grau^[6]

Uma função quadrática é definida como uma função que apresenta o expoente 2 como maior expoente das variáveis. O seu gráfico é constituído por uma parábola. É expressa por:^[2][4]

${\displaystyle f(x)=ax^{2}+bx+c.}$

Por exemplo,

${\displaystyle y=4x^{2}+2x+1\rightarrow }$ o grau é 2 e é composto de três monômios.

Funções polinomiais de outros graus

• ${\displaystyle f(x)=2\rightarrow }$ não há variável, mas pode-se considerar que o grau é zero. Esta é uma função constante.^[2][4]
• ${\displaystyle f(x)=0\rightarrow }$ neste caso, é conveniente dizer que não há grau, ou que o grau é negativo (menos infinito).
• ${\displaystyle f(x)=(1/2)x^{4}-7x^{3}+(4/5)\rightarrow }$ é uma função polinomial de grau 4. Neste caso: ${\displaystyle a_{0}=4/5,a_{1}=0,a_{2}=0,a_{3}=-7,a_{4}=1/2.}$

Função constante

Gráfico de uma função constante

Define-se função constante por :^[2][4]

Dado um número ${\displaystyle k,}$

${\displaystyle f(x)=k,\forall x\in Dom(f)}$

${\displaystyle Im(f)=\{k\}}$

Ou seja, o valor da imagem será sempre o mesmo, independente do valor do ${\displaystyle x.}$

O gráfico de uma função constante é uma reta paralela ao eixo ${\displaystyle x.}$;

Polinômios especiais

• Polinómios de Bernstein
• Polinômio característico
• Polinômios de Laguerre
• Polinômios de Tchebychev
• Polinômios de Legendre
• Polinômios de Hermite
• Polinómio de Newton
• Polinômio de Hurwitz
• Polinômio de Lagrange
• Polinômio irredutível
• Polinômio homogêneo

Ver também

• Monômio
• Cálculo com polinômios
• Série de potências
• Coeficiente
• Divisão polinomial
• Fatoração polinomial
• Função racional
• Frações parciais
• Fórmulas de Viète
• Equação algébrica

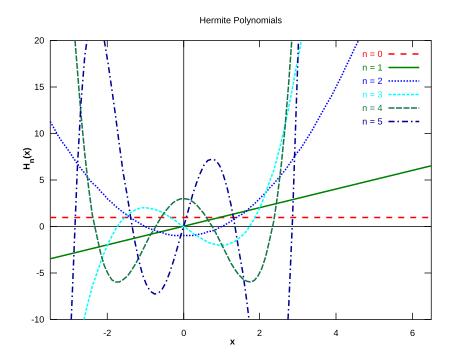
Polinômios de Hermite

Origem: Wikipédia, a enciclopédia livre.

Os polinômios de Hermite são um exemplo de polinômios ortogonais cujo principal campo de aplicação encontra-se na mecânica quântica, especialmente no estudo do oscilador harmônico unidimensional. São nomeados assim em homenagem a Charles Hermite.

Os cinco primeiros polinômios de Hermite (probabilísticos).

• 
  

Definição

Os polinômios de Hermite ("polinômios de Hermite probabilísticos") são definidos por:

${\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}/2}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}/2}\,\!}$

Ou, às vezes, por ("polinômios de Hermite físicos")

${\displaystyle H_{n}^{\mathrm {phys} }(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}\,\!}$

Essas definições não são exatamente equivalentes: uma é o redimensionamento da outra:

${\displaystyle H_{n}^{\mathrm {phys} }(x)=2^{n/2}H_{n}^{\mathrm {prob} }({\sqrt {2}}\,x)\,\!}$.

Os polinômios físicos podem ser escritos como:

${\displaystyle H_{n}^{\mathrm {phys} }(x)=(2x)^{n}-{\frac {n(n-1)}{1!}}(2x)^{n-2}+{\frac {n(n-1)(n-2)(n-3)}{2!}}(2x)^{n-4}-\dots }$

• Teorema do resto
• Anel de polinômios
• Lema de Gauss
• Critério de Eisenstein
• Interpolação polinomial