TOPOGEOMETRIA GRACELI EM HARMÔNICOS ESFÉRICOS E ESTOCÁSTICOS E ALEATÓRIOS

 

Harmônicos esféricos

Representações visuais dos primeiros harmônicos esféricos. Partes em azul e amarelo representam, respectivamente, as regiões nas quais a função é positiva e negativa.

Em matemática e ciência física, harmónicos esféricos são funções harmónicas que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Os harmónicos esféricos são importantes em muitas aplicações teóricas e práticas, particularmente em física atómica (uma vez que a função de onda do electrão contém harmónicos esféricos) e na teoria do potencial, tanto no campo gravitacional como na eletrostática.

• 
  

Introdução

Harmónicos esféricos de variável real Y_lm, para l =0,...,4 (de cima para baixo) e m = 0,...,4 (da esquerda para a direita). Os harmónicos Y_l-m com m negativo são idênticos, mas com uma rotação de 90º/m em torno do eixo z em relação aos harmónicos positivos.

A equação de Laplace em coordenadas esféricas é dada por:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

(Ver também Nabla e laplaciano em coordenadas esféricas). Se nesta expressão considera-se soluções específicas da forma ${\displaystyle f(r,\theta ,\phi )=R(r)Y(\theta ,\varphi )}$, a parte angular Y é chamada harmónico esférico e satisfaz a relação

${\displaystyle {1 \over \sin \theta }{d \over d\theta }\left(\sin \theta {dY(\theta ,\varphi ) \over d\theta }\right)+{1 \over \sin ^{2}\theta }{d^{2}Y(\theta ,\varphi ) \over d\varphi ^{2}}+l(l+1)Y(\theta ,\varphi )=0}$

Se, por sua vez, utiliza-se o método de separação de variáveis para esta equação, pode-se ver que a equação acima admite soluções periódicas nas duas coordenadas angulares (l é um inteiro). Logo, a solução periódica do sistema anterior depende de dois inteiros (l, m) e é dada em termos de funções trigonométricas e dos polinômios associados de Legendre:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta })}$

Onde: ${\displaystyle Y_{\ell }^{m}}$ é chamada de função harmónica esférica de grau ${\displaystyle \ell }$ e ordem ${\displaystyle m}$; ${\displaystyle P_{\ell }^{m}}$ é o polinómio associado de Legendre; ${\displaystyle N}$ é uma constante de normalização; e ${\displaystyle \theta }$ e ${\displaystyle \varphi }$ representam os parâmetros angulares (respectivamente, o ângulo azimutal ou colatitude e o ângulo polar ou longitude).

As coordenadas esféricas utilizadas neste artigo são consistentes com àquelas usadas pelos físicos, mas diferem das utilizadas pelos matemáticos (ver coordenadas esféricas). Em particular, a colatitude ${\displaystyle \theta }$, ou ângulo polar, assume valores de ${\displaystyle 0\leq \theta \leq \pi }$ e a longitude ${\displaystyle \varphi }$, ou azimute, está na faixa de ${\displaystyle 0\leq \varphi <2\pi }$. Portanto, ${\displaystyle \theta }$ é nulo no Pólo Norte, ${\displaystyle \pi /2}$ no Equador e ${\displaystyle \pi }$ no Pólo Sul.

Quando a equação de Laplace é resolvida em coordenadas esféricas, as condições de periodicidade na fronteira da coordenada ${\displaystyle \varphi }$ e as condições de regularidades nos "Pólos Norte e sul" da esfera condizem com o que foi dito que os números l e m necessários devem ser inteiros que satisfazem ${\displaystyle \ell \geq 0}$ e ${\displaystyle |m|\leq \ell }$.

Normalização

Há várias normalizações utilizadas para as funções harmónicas esféricas. Em física e sismologia essas funções são geralmente definidas como

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=A_{\ell }^{m}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

onde

${\displaystyle A_{\ell }^{m}={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}}$

Estas funções são ortonormalizadas,

${\displaystyle \int _{\varphi =0}^{2\pi }d\varphi \int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$,

onde δ_aa = 1, δ_ab = 0 se a ≠ b (ver delta de Kronecker). Nas áreas de geodésia e análise espectral utiliza-se

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possui um termo linear

${\displaystyle {1 \over 4\pi }\int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$.

No magnetismo, no entanto, usa-se os harmónicos de Schmidt semi-normalizados,

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {(\ell -m)! \over (\ell +m)!}}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possuem a seguinte normalização:

${\displaystyle \int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,={4\pi \over (2\ell +1)}\delta _{\ell \ell '}\,\delta _{mm'}}$.

Utilizando a identidade (ver funções associadas de Legendre)

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}}$

pode-se demonstrar que todas as funções harmónicas esféricas normalizadas acima satisfazem

${\displaystyle Y_{\ell }^{m*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi )}$,

onde o símbolo * significa conjugação complexa.

Convenção de fase de Condon-Shortley

Um forte motivo para uma confusão com a definição de harmónicos esféricos é o fator de fase ${\displaystyle (-1)^{m}\,}$, normalmente identificado como a fase de Condon-Shortley na literatura quântica. Na mecânica quântica, é uma prática usual incluir este fator de fase na definição das funções associadas de Legendre, ou anexá-lo à definição de funções harmónicas esféricas. Não há nenhuma exigência da utilização da fase de Condon-Shortley na definição de funções harmónicas esféricas, mas se ela for incluída, então algumas operações no domínio da mecânica quântica serão mais simples. No magnetismo e na geodésia, ao contrário, nunca incluiu-se o fator de fase Condon-Shortley na definição dos harmónicos esféricos.

Expansão em harmónicos esféricos

Os harmónicos esféricos formam um conjunto completo ortonormal de funções e, portanto, formam um espaço vetorial análogo aos vetores unitários da base. Na esfera unitária, todas as funções de quadrado integrável podem, portanto, ser expandidas como uma combinação linear de:

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,Y_{\ell }^{m}(\theta ,\varphi )}$.

Essa expansão é exata sempre que ${\displaystyle \ell }$ estende-se até o infinito. Haverá um erro de truncamento ao limitar a soma sobre ${\displaystyle \ell }$ numa largura de banda finita ${\displaystyle L}$. Os coeficientes da expansão ${\displaystyle f_{\ell }^{m}}$ podem ser obtidos multiplicando-se a equação pelo conjugado complexo dos harmónicos esféricos, integrando-se sobre um ângulo sólido ${\displaystyle \Omega \!\,}$ e usando-se as relações de ortogonalidade acima. No caso de harmónicos ortonormalizados, obtemos

${\displaystyle f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )d\Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \sin \theta f(\theta ,\varphi )Y_{\ell }^{m*}(\theta ,\varphi )}$.

Um conjunto alternativo de harmónicos esféricos para funções reais pode ser obtido a partir do conjunto

${\displaystyle Y_{\ell m}={\begin{cases}Y_{\ell }^{0}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad {\mbox{ si }}m=0\\{1 \over {\sqrt {2}}}\left(Y_{\ell }^{m}+(-1)^{m}\,Y_{\ell }^{-m}\right)={\sqrt {2}}NP_{\ell }^{m}(\theta )\cos m\varphi \qquad \quad \quad {\mbox{si }}m>0\\{1 \over i{\sqrt {2}}}\left(Y_{\ell }^{|m|}-(-1)^{|m|}\,Y_{\ell }^{-|m|}\right)={\sqrt {2}}NP_{\ell }^{|m|}(\theta )\sin |m|\varphi \quad {\mbox{ si }}m<0.\end{cases}}}$

Estas funções têm as mesmas propriedades que as funções de normalização complexas dadas anteriormente. Nesta forma, uma função real integrável pode ser expressa como uma soma infinita de harmónicos esféricos

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{lm}\,Y_{lm}(\theta ,\varphi )}$.

Harmónicos esféricos em física

Seguem-se algumas aplicações dos harmónicos esféricos na física, tanto na eletrostática como na mecânica quântica.

Harmónicos esféricos na eletrostática

O átomo de hidrogênio

Ver artigo principal: Átomo de Hidrogênio

O modelo quântico moderno do átomo de hidrogênio assume o elétron em um estado constante de energia tem sua posição distribuída ao redor do núcleo atômico como uma distribuição de probabilidades, cuja variação angular é dada por um harmónico esférico.

Análise espectral

A potência total de uma função ${\displaystyle f}$ é definida na linguagem de processamento de sinais eletrônicos como sendo a integral do quadrado da função dividida pela área varrida por ela. Usando as propriedades de ortonormalização de funções harmónicas esféricas de potência real unitária, é fácil verificar que a potência total de uma função definida na esfera unitária está relacionada aos seus coeficientes espectrais através de uma generalização do teorema de Parseval:

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{l=0}^{\infty }S_{f\!f}(l)}$,

onde

${\displaystyle S_{f\!f}(l)=\sum _{m=-l}^{l}f_{lm}^{2}}$

é definido como o espectro de potência angular. Da mesma forma, pode-se definir a potência cruzada entre duas funções como

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g(\Omega )\,d\Omega =\sum _{l=0}^{\infty }S_{fg}(l)}$,

onde

${\displaystyle S_{fg}(l)=\sum _{m=-l}^{l}f_{lm}g_{lm}}$

é definido como o espectro cruzado neste caso. Se as funções ${\displaystyle f}$ e ${\displaystyle g}$ possuem valor médio igual a zero (ou seja, com coeficientes espectrais ${\displaystyle f_{00}}$ e ${\displaystyle g_{00}}$ nulos), então ${\displaystyle S_{f\!f}(l)}$ e ${\displaystyle S_{fg}(l)}$ representam as contribuições para a variância e covariância da função para ${\displaystyle \ell }$, respectivamente. É comum que o espectro de potência cruzado seja aproximado por uma lei de potências do tipo

${\displaystyle S_{f\!f}(l)=C\,\ell ^{\beta }}$.

Quando ${\displaystyle \beta =0}$, o espectro é "branco", pois cada nível tem potências iguais. Quando ${\displaystyle \beta <0}$, o espectro é chamado de "vermelho", porque não há mais energia nos níveis mais baixos com comprimentos de onda mais longos do que nos níveis mais elevados. Finalmente, quando ${\displaystyle \beta >0}$, o espectro é chamado de "azul".

Teorema da adição

Um resultado matemático de grande interesse e utilidade é chamado teorema da adição para harmónicos esféricos. Se dois vetores r e r' tem coordenadas esféricas ${\displaystyle (r,\theta ,\varphi )}$ e ${\displaystyle (r',\theta ',\varphi ')}$, respectivamente, o ângulo ${\displaystyle \gamma }$ entre eles é dado pela expressão

${\displaystyle \cos \gamma =\cos \theta \cos \theta '+\sin \theta \sin \theta '\cos(\varphi -\varphi ')}$.

O teorema da adição expressa um polinômio de Legendre de ordem ${\displaystyle l}$ no ângulo ${\displaystyle \gamma }$ em termos de produtos de dois harmónicos esféricos com coordenadas angulares ${\displaystyle (\theta ,\varphi )}$ e ${\displaystyle (\theta ',\varphi ')}$:

${\displaystyle P_{l}(\cos \gamma )={\frac {4\pi }{2l+1}}\sum _{m=-l}^{l}Y_{lm}^{*}(\theta ',\phi ')\,Y_{lm}(\theta ,\varphi )}$.

Esta expressão é válida tanto para harmónicos reais como complexos. Entretanto, deve-se ressaltar que a fórmula apresentada anteriormente é válida apenas para harmónicos esféricos ortonormalizados. Harmónicos de potência unitária são necessários para eliminar o fator ${\displaystyle 4\pi }$ da expressão anterior.

Visualizando os harmónicos esféricos

Representação esquemática de Y_lm sobre a esfera unitária. Y_lm é igual a 0 ao longo de m círculos que passam pelos polos e ao longo de l-m círculos de mesma latitude. A função muda de sinal cada vez que cruza uma dessas linhas.

A função harmónica esférica real Y₃₂ mostrada ao longo de quatro cortes.

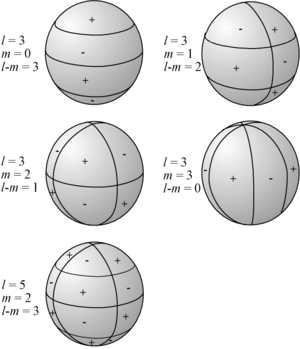
Os harmónicos esféricos são facilmente visualizados através da contagem do número de cruzamentos que ambos estão na direção das coordenadas ${\displaystyle \theta }$ e ${\displaystyle \varphi }$. Para obter a orientação sobre ${\displaystyle \theta }$, as funções associadas de Legendre possuem ${\displaystyle l-|m|}$ zeros, enquanto que na coordenada ${\displaystyle \varphi }$ as funções trigonométricas seno e cosseno possuem ${\displaystyle 2|m|}$ zeros.

Quando o harmónico esférico de ordem ${\displaystyle m}$ é nulo, as funções harmónicas esféricas não dependem de ${\displaystyle \varphi }$, e diz-se que a função é zonal. Quando ${\displaystyle l=|m|}$, não existem zeros na direção ${\displaystyle \theta }$, e diz-se que a função é setorial. Nos outros casos, as funções formam um padrão em xadrez sobre a esfera.

Expressões analíticas para os primeiros harmónicos esféricos

Eis as expressões analíticas dos primeiros harmónicos esféricos ortonormalizados, com a convenção de fase de Condon-Shortley:

${\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}$

${\displaystyle Y_{1}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{-i\varphi }}$

${\displaystyle Y_{1}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over \pi }}\,\cos \theta }$

${\displaystyle Y_{1}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{-2i\varphi }}$

${\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{-i\varphi }}$

${\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\,(3\cos ^{2}\theta -1)}$

${\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{2i\varphi }}$

${\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\,(5\cos ^{3}\theta -3\cos \theta )}$

Ver também: [[:[[Tabela de harmónicos esféricos até Y₁₀]]]]

Teoria matemática geral

O conjunto dos harmónicos esféricos pode ser visto como uma representação da simetria do grupo das rotações em torno de um ponto SO(3) e das aplicações universais SU(2). Portanto, ele capta a simetria da esfera em duas dimensões. Cada grupo de harmónicos esféricos, com um dado valor do parâmetro l leva a uma representação diferente irredutível do grupo SO(3).

Além disso, a área é equivalente à esfera de Riemann. O conjunto completo das simetrias da esfera de Riemann é descrito pelo grupo das transformações de Möbius PSL(2,C), que é isomorfo ao grupo de Lie real chamado grupo de Lorentz. O análogo dos harmónicos esféricos em relação ao grupo de Lorentz é a série hipergeométrica; na verdade, os harmónicos esféricos podem ser reescritos em termos da série hipergeométrica, já que SO(3) é um subgrupo de PSL(2,C).

Mais especificamente, pode-se generalizar a série hipergeométrica para descrever as simetrias de qualquer espaço de simetria. Em particular, a série hipergeométrica pode ser estendida para todos os grupos de Lie.^[1][2][3][4]

Estocástico

Origem: Wikipédia, a enciclopédia livre.

Esta página cita fontes, mas estas não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável poderá ser removido.—Encontre fontes: Google (notícias, livros e acadêmico) (Janeiro de 2017)

Em teoria probabilística, o padrão estocástico é aquele cujo estado é indeterminado, com origem em eventos aleatórios. Por exemplo, o lançar de dados resulta num processo estocástico, pois qualquer uma das 6 faces do dado tem iguais probabilidades de ficar para cima após o arremesso. Assim, qualquer sistema ou processo analisado usando a teoria probabilística é estocástico, ao menos em parte.

Porém, é importante salientar uma diferença entre aleatoriedade estatística e estocasticidade. Normalmente, os eventos estocásticos são estatisticamente aleatórios. Todavia, podem eventualmente não o ser. É perfeitamente plausível, embora improvável, que uma série de 10 arremessos de dados gere a seqüência não aleatória de 6,5,4,3,2,1,2,3,4,5 ou 1,1,1,1,1,1,1,1,1,1. Apesar de coerente — ou compressível (podendo ser expressa de um modo mais comprimido que a seqüência inteira) — a seqüência estatisticamente não-aleatória é estocástica, pois surgiu através de um evento aleatório: o lançar de dados.

Há também a música estocástica, forma de composição baseada em padrões estocásticos, utilizando-se de computadores para redigir as partituras. Tem como maior ícone o compositor grego Iannis Xenakis.

O termo Estocástico também é usado para descrever uma ferramenta estatística de análise de mercado muito utilizada em estudos do mercado de ações:

"O Estocástico é um oscilador desenvolvido por George Lane no início da década de 1950, sendo muito utilizado por investidores com perfil de curto prazo ou que operam com derivativos, como opções de compra. Ele se baseia no princípio de que os preços de fechamento, durante uma tendência de alta, tendem a se posicionar mais próximos da máxima do dia do que de sua mínima. De forma análoga, durante uma tendência de baixa, o fechamento posiciona-se mais próximo da mínima do que da máxima. Seus sinais de compra e venda estão associados à identificação de níveis de sobrecompra e sobrevenda dos ativos"^[1]

Sistemas e processos estocásticos desempenham um papel fundamental em modelos matemáticos de fenômenos em muitos campos da ciência, engenharia e economia.

Teoria matemática

Em matemática, especificamente dentro da teoria da probabilidade, o campo dos processos estocásticos tem se tornado uma importante área de pesquisa.

Uma matriz estocástica é uma matriz que tem números reais não-negativos cuja soma dos termos de cada coluna é 1.

Inteligência artificial

Dentro da inteligência artificial, programas estocásticos trabalham usando métodos probabilísticos para solucionar problemas, como em redes neurais estocásticas, otimização estocástica e algoritmos genéticos. Um problema pode ser estocástico em si mesmo, como no planejamento sob incerteza.

Ciências naturais

Um exemplo de processo estocástico no mundo natural é a pressão de um gás, como modelado no processo de Wiener. Mesmo que cada molécula esteja se movendo segundo uma trajetória determinística (segundo a física clássica), o movimento de um conjunto delas é computacionalmente imprevisível. Um conjunto suficientemente numeroso de moléculas exibirá características estocásticas, como o preenchimento do recipiente, existindo pressão igual, difundindo-se ao longo de diferentes gradientes de concentração. Essas são as propriedades emergentes do sistema.

Física

O nome "Monte Carlo" para o método estocástico de Monte Carlo foi popularizado pelos físicos pesquisadores Stanisław Ulam, Enrico Fermi, John von Neumann, e Nicholas Metropolis além de outros. O nome é uma referência ao Casino Monte Carlo em Mônaco onde o tio de Ulam iria pedir dinheiro para jogar. O uso da aleatoriedade e a natureza repetitiva dos processos são análogos às atividades conduzidas no casino.

Música estocástica

Na música, elementos estocásticos podem ser produzidos por processos matemáticos. Processos estocásticos na composição de partes fixas ou dos sons durante a execução. Um dos pioneiros da música estocástica foi Iannis Xenakis, ele usava probabilidade, teoria dos jogos, teoria dos grupos, teoria dos conjuntos e álgebra de Boole, usando também computadores para produzir as melodias.

A palavra aleatoriedade exprime quebra de ordem, propósito, causa, ou imprevisibilidade em uma terminologia não científica. Um processo aleatório é o processo repetitivo cujo resultado não descreve um padrão determinístico, mas segue uma distribuição de probabilidade.^[1]

Quando não se está explicitamente anunciado qual distribuição de probabilidade está sendo usada, supõe-se que seja uma distribuição normal, o que acarreta o fato de que "número aleatório", assim descrito, é formado como uma sequência de números onde para o próximo número existe uma igual probabilidade de ocorrer qualquer dos elementos do conjunto universo.^[2]

O termo aleatório é frequentemente utilizado em estatística para designar uma propriedade estatística bem definida tal como um a quebra de uma neutralidade ou correlação.

Índice

• 1História
• 2Aleatoriedade em ciências
  • 2.1Nas ciências físicas
• 3Ver também
• 4Referências
• 5Ligações externas

História

Afresco antigo de jogadores de dados em Pompeia.

Na história antiga, os conceitos de chance e de aleatoriedade eram interligados ao conceito que era atribuído a destino. Várias pessoas da antiguidade jogavam dados para determinarem o destino, e posteriormente isso se desenvolveu em jogos de azar. A maioria das culturas usaram vários métodos de adivinhações para tentarem contornar a aleatoriedade e o destino, ou mesmo a dita sorte.^[3]

Os chineses foram talvez o povo que definiu chances e probabilidade mais cedo, 3 000 anos atrás. Os filósofos gregos discutiram aleatoriedade por muito tempo, mas somente de formas não quantitativas. Foi só no século XVI que matemáticos italianos começaram a definir probabilidades associadas a vários jogos de azar. A invenção do cálculo teve um impacto positivo no estudo formal da aleatoriedade. Na edição de 1888 de seu livro The Logic of Chance (A lógica da chance) John Venn escreveu um capítulo sobre "O conceito de aleatoriedade (The conception of randomness)" que incluía sua explicação sobre a aleatoriedade dos algarismos do número Pi ao usá-los para construir um passeio aleatório em duas dimensões.^[4]

Aleatoriedade em ciências

Ver também: Pseudoaleatoriedade

Muitos campos científicos são relacionados a aleatoriedade:

Nas ciências físicas

No século XIX, cientistas utilizaram da ideia de movimentos aleatórios de moléculas no desenvolvimento da mecânica estatística de modo a explicar fenômenos na termodinâmica e propriedades dos gases.^[5]

De acordo com diversas interpretações da mecânica quântica, fenômenos microscópicos são objetivamente aleatórios. Isto é, um experimento onde todos os parâmetros relevantes são controlados, ainda existem alguns aspectos do resultado que variam aleatoriamente. Um exemplo de tal experimento é tomando um único átomo instável em um meio controlado; não se pode prever quanto tempo levará para que o átomo decaia; apenas a probabilidade do decaimento com um dado tempo é que pode ser calculado.^[6] Assim, a mecânica quântica não especifica o resultado de experimentos individuais, mas apenas as probabilidades. Teoria de variáveis ocultas procuram desenvencilhar-se do ponto de vista que a natureza contem aleatoriedade irredutível: tais teorias pressupõe, que em um processo que aparenta ser aleatório, propriedades não observáveis (ocultas) com certa distribuição estatística são, de algum modo, as responsáveis por determinar o resultado em cada caso.^[7][8]

Processo estocástico

Origem: Wikipédia, a enciclopédia livre.

Flutuações nos mercados de ações podem ser modeladas por processos estocásticos.

Dentro da teoria das probabilidades, um processo estocástico é uma família de variáveis aleatórias representando a evolução de um sistema de valores com o tempo. É a contraparte probabilística de um processo determinístico. Ao invés de um processo que possui um único modo de evoluir, como nas soluções de equações diferenciais ordinárias, por exemplo, em um processo estocástico há uma indeterminação: mesmo que se conheça a condição inicial, existem várias, por vezes infinitas, direções nas quais o processo pode evoluir.

Em casos de tempo discreto, em oposição ao tempo contínuo, o processo estocástico é uma sequência de variáveis aleatórias, como por exemplo uma cadeia de Markov. As variáveis correspondentes aos diversos tempos podem ser completamente diferentes, o único requisito é que esses valores diferentes estejam todos no mesmo espaço, isto é, no contradomínio da função. Uma abordagem possível é modelar as variáveis aleatórias como funções aleatórias de um ou vários argumentos determinísticos, na maioria dos casos, em relação ao parâmetro do tempo. Apesar de os valores aleatórios de um processo estocástico em momentos diferentes parecerem variáveis aleatórias independentes, nas situações mais comuns, eles exibem uma complexa dependência estatística.

Exemplo de processos estocásticos incluem flutuações nos mercados de ações e nas taxas de câmbio, dados médicos como temperatura, pressão sanguínea e variações nos potenciais elétricos do cérebro registrados em um eletroencefalograma, fluxo turbulento de um líquido ou gás, variações no campo magnético da Terra, mudanças aleatórias no nível de sinais de rádio sintonizados na presença de distúrbios meteorológicos, flutuação da corrente em um circuito elétrico na presença de ruído térmico, movimentos aleatórios como o movimento Browniano ou passeios aleatórios, entre outros.

Uma generalização de um processo estocástico, o campo aleatório é definido ao permitir que as variáveis sejam parametrizadas por membros de um espaço topológico ao invés do tempo. Exemplos de campos aleatórios incluem imagens de estática, topografia, ondas de superfície e variações na composição de um material heterogêneo.

Mais genericamente, seguindo Kac^[1] e Nelson,^[2] qualquer tipo de evolução temporal, determinística ou essencialmente probabilística, que seja analisável em termos de probabilidade pode ser chamada de processo estocástico.

• 
  

Definição formal e propriedades básicas

Definição

Dado um espaço de probabilidade ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ e um espaço mensurável ${\displaystyle (S,\Sigma )}$, um processo estocástico de valor S é um conjunto de variáveis aleatórias de valor S em ${\displaystyle \Omega }$, indexadas por um conjunto totalmente ordenado T ("tempo"). Isto é, um processo estocástico X é um conjunto

${\displaystyle \{X_{t}:t\in T\}}$

onde cada ${\displaystyle X_{t}}$ é uma variável de aleatória de valor S em ${\displaystyle \Omega }$. O espaço S é então chamado de espaço de estados do processo.

Distribuições de dimensões finitas

Seja X um processo estocástico de valor S. Para cada sequência finita de ${\displaystyle T'=(t_{1},\ldots ,t_{k})\in T^{k}}$, o k-ésimo ${\displaystyle X_{T'}=(X_{t_{1}},X_{t_{2}},\ldots ,X_{t_{k}})}$ é uma variável aleatória tendo valores em ${\displaystyle S^{k}}$. A distribuição ${\displaystyle \mathbb {P} _{T'}(\cdot )=\mathbb {P} (X_{T'}^{-1}(\cdot ))}$ dessa variável aleatória é uma probabilidade medida em ${\displaystyle S^{k}}$. Isso é chamado uma distribuição finita de X. Sob restrições topológicas adequadas, uma coleção “consistente” de distribuições de dimensões finitas pode ser usada para definir um processo estocástico.

Movimento browniano de uma partícula num fluido. A partícula é apenas um ponto, do tamanho de todos os presentes na imagem, a área amarela serve para que se possa observar as setas - vetores aceleração - que são recebidos pela partícula em questão quando ela se choca com as outras partículas do fluido.